Nouns by Tag math
Marcus Terentius Varro (Varro Reatinus)
Ancient Roman historian best known for his Varronian chronology of the Roman Republic including his date of the foundi...
Hypatia
Hypatia (c. 360 – 415) was a Greek philosopher and mathematician who served as head of the Platonist school in Alexandria...
Nasīr al-Dīn Tūsī (Muhammad ibn al-Hasan al-Tūsī)
Ccreator of trigonometry as a distinct mathematical discipline
Leonard Digges
16th century English scientist who invented a functioning telescope sometime between 1540 and 1559According to son, Thoma...
John Dee
Devoted much of his life to the study of alchemy, divination, and Hermetic philosophy. Also, as spy/advisor to Queen Elizabet...
Johannes Kepler
Keplers Laws of Planetary Motion:- The orbit of a planet is an ellipse with the Sun at one focus.
- A line se...
La Géométrie (Geometry)
First work to propose the idea of uniting algebra and geometry into a single subject, thereby inventing analytic geometry, wh...
Isaac Newton
Most famous for discovering the Law of Gravity, the Calculus, and other scientific and mathematical advances, but he spent mo...
Gottfried Wilhelm Leibniz (von Leibnitz)
A prominent German polymath and one of the most important logicians, mathematicians and natural philosophers of the Enlighten...
Jacob Bernoulli
17th century Swiss mathematician who solidified many concepts of modern probability theory and also discovered the mathematic...
Leonhard Euler
Prolific Swiss mathematician, physicist, astronomer, geographer, logician and engineer — one of the most eminent mathem...
Gustav Kirchhoff (Gustav Robert Kirchhoff)
German physicist famous for several sets Kirchhoff's Laws- Kirchhoff's circuit laws
- Kirchhof...
J. J. Thomson (Sir Joseph John)
British physicist and Nobel Laureate in Physics, credited with the discovery of the electron, the first subatomic particle to...
Heinrich Rudolf Hertz
Nineteenth century German physicist who proved the existence of the electromagnetic waves.When asked about the applicatio...
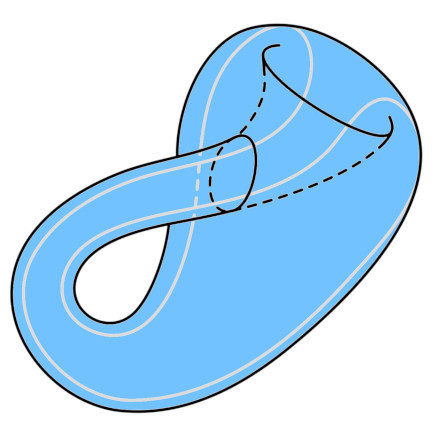
Klein bottle
A one-sided surface conceived as a 3D mobius strip. If traveled upon, the traveler may visit the inside as well as outside.
Max Born
20th century German-Jewish physicist and mathematician instrumental in the development of quantum mechanics
Kurt Gödel
Gödel essentially constructed a formula that claims that it is unprovable in a given formal system. If it were provable, it ...