Ptolemy's Almagest
150 AD published
Originally titled "Μαθηματικὴ Σύνταξις" (Mathēmatikē Syntaxis) in Ancient Greek, and also called Syntaxis Mathematica or Almagestum in Latin
Ptolemy set up a public inscription at Canopus, Egypt, in 147 or 148. N. T. Hamilton found that the version of Ptolemy's models set out in the Canopic Inscription was earlier than the version in the Almagest. Hence it cannot have been completed before about 150, a quarter-century after Ptolemy began observing.
Subjects Who or What published?
-
Ptolemy (Claudius Ptolemy, Κλαύδιος Πτολεμαῖος) The preeminent astronome...
Objects To Whom or What was published?
-
Almagest (Μαθηματικὴ Σύνταξις, Syntaxis Mathematica) Ptolemy presents his geo...
Timelines (that include this event)
Attachments
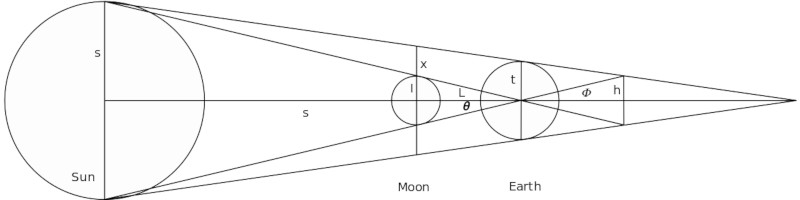
Geometric construction used by Hipparchus In Almagest V, 11, Ptolemy writes: Now Hipparchus made such an examination principally from the sun. Since from other properties of the sun and moon (of which a study will be made below) it follows that if the distance of one of the two luminaries is given, the distance of the other is also given, he tries by conjecturing the distance of the sun to demonstrate the distance of the moon. First, he assumes the sun to show the least perceptible parallax to find its distance. After this, he makes use of the solar eclipse adduced by him, first as if the sun shows no perceptible parallax, and for exactly that reason the ratios of the moon's distances appeared different to him for each of the hypotheses he set out. But with respect to the sun, not only the amount of its parallax, but also whether it shows any parallax at all is altogether doubtful.
astronomy
math
Events in 150 MORE